| << Vissza |
| A fraktálok természete 1. | ||||||||
| Teimel - 2007-08-30 14:24:00 | ||||||||
| Tudomány | ||||||||
|
Ebben a cikkben bemutatom a fraktál geometria történetét, és pár jellegzetességét, a "felfedezésétől" kezdve egészen a tudományban, ill. a művészetben való felhasználásáig.
*** Mi az a fraktál? :)
A fraktál olyan alakzat, amely változó nagyítási ráták mellett önismétlődést mutat. Más szavakkal, ha felnagyítjuk egy fraktál egy részét, a nagyított képben észrevehetünk egy, az eredetihez hasonló, kisebb fraktált.
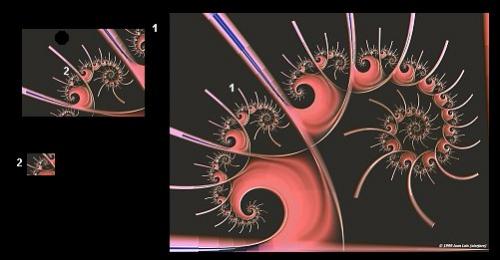
1. ábra: Julia fraktál
A fraktálok egy másik, nagyon fontos jellemzője a tört dimenzió. Ahelyett, hogy egy, kettő, vagy három dimenziójuk lenne (mint az ismertebb alakzatoknak), a legtöbb fraktálnak olyan dimenziói vannak, amelyek nem illeszkednek bele ebbe a koncepcióba. Mi több, a dimenziójuk csak ritkán írható le egész számmal. Pontosan ez áll a nevük hátterében.
Általában a fraktálok megfelelnek az előbbiekben meghatározott definíciónak. Néha viszont előfordul, hogy új és eltérő jellegzetességek bukkannak elő olyan helyen, ahol máskülönben egy minta ismétlődésének kellene lennie. Ez attól függ, hogy milyen fraktált vizsgálunk, és persze attól is, hogy milyen egyenlet képezte azt.
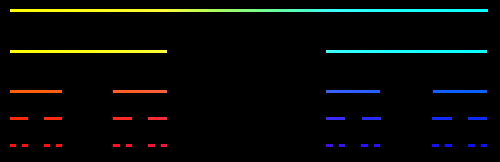
2 ábra: Cantor-por
A Cantor-port, a történelem valószínűsíthetően első igazi fraktálját Georg Cantor német matematikus (a halmazelmélet szülőatyja) írta le 1872 körül. Egy egyszerű ábráról van szó, de minden eddig említett jellemzővel rendelkezik. Minden szinten ismétli önmagát, és tört dimenziója van, melynek értéke: 0.630929753571457437099527114! (helyesebben log 2/log 3). Az ábrán megfigyelhető a fraktálok másik alapvető jellegzetessége: iterációval képződnek.
Az iteráció úgy írható le, mint egy visszacsatoló folyamat, amely n-szer ismétlődik. Elvégzi egy bizonyos funkció számításait, amely egy eredményt, output-ot képez, amely ugyanazon funkció következő számításának lesz a kezdő értéke, azaz input-ja. Az eljárás egyre és egyre ismétlődik (akár végtelenszer), egy iterációt képezve. Ilyen folyamat alkot egy fraktált.
A Cantor-por példáján, egy nagy szegmenssel kezdünk (az iniciátor), felosztjuk három egyenlő részre, majd kivesszük a középsőt. Ez a folyamat (a generátor) végtelen sokszor végrehajtódik, létrehozva ezzel a Cantor-port.
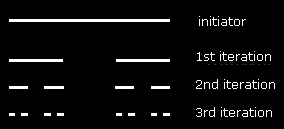
3. ábra: A Cantor-por iterációja
Hasonló módon képezhetjük a Sierpinski háromszöget, amelyet egy lengyel matematikus, Waclaw Sierpinski jegyzett le 1915-ben:

4. ábra: Sierpinski háromszög
Egy egyenlő oldalú háromszöggel kezdünk. Rajzoljunk bele egy ugyancsak egyenlő oldalú háromszöget, s legyenek a csúcsai a nagy háromszög oldalfelező pontjain. Ezután vegyük ki az új háromszöget, s így három egyenlő oldalú háromszög marad a nagyon belül. Ismételjük meg az eljárást minden kisebb háromszögön, s eredményül a Sierpinski háromszöget kapjuk majd.
5. ábra: A Sierpinski háromszög iterációja
Persze a "vegyük ki a háromszöget" nem azt jelenti, hogy csak úgy egyszerűen vegyük ki, hanem azt, hogy annak a bizonyos háromszögnek a pontjai nem részei a pontoknak, amelyek a Sierpinski háromszöget alkotják.
Habár a fraktálok a 19. század vége felé már ismertek voltak (úgy tekintettek rájuk, mint matematikai érdekességekre), a közöttük lévő kapcsolatot kétség kívül Benoît Mandelbrot és más termékeny elméjű tudósok 60-as és 70-es években tett kutatásai fedték fel.
További elmélkedés a fraktálok dimenzióiról
A geometriában a pontnak nincs dimenziója, mivel nincs hosszúsága, szélessége, ill. mélysége. .
6. ábra: A pont
Az egyenesnek 1 dimenziója van, mivel van hosszúsága.
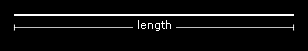
7. ábra: az egyenes
A sík 2 dimenziós, mivel van hosszúsága és szélessége.
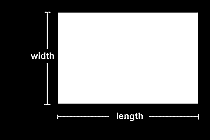
8. ábra: a sík
A kocka 3 dimenziós, mivel van szélessége, hosszúsága, és mélysége.
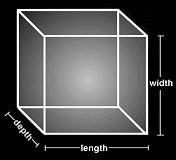
9. ábra: a kocka
Az eddigiek beleférnek abba a koncepcióba, amit általában dimenziónak nevezünk (euklédeszi, vagy topológiai dimenzió). A fraktáloknak viszont tört dimenzióik vannak, általában nem egész számok, mint pl 1.7, 0.5326478 vagy 3.28. Hogyan is lehet ez?
Ha megfelezünk egy egydimenziós alakzatot, akkor az eredeti alakzat két kisebb mását kapjuk. 10. ábra: az egyenes felosztása
Ha megfelezünk egy kétdimenziós alakzatot először a hosszúsága, majd a szélessége mentén, akkor négy, az eredetihez hasonló alakzatot kapunk.
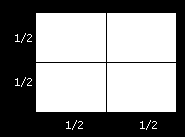
11. ábra: a sík felosztása
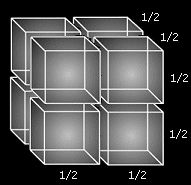
Ha megfelezünk egy háromdimenziós alakzatot először a hosszúsága, majd a szélessége, végül a mélysége mentén, akkor nyolc, az eredetihez hasonló alakzatot kapunk.
12. ábra: a kocka felosztása Közelebbről megnézve megállapítható, hogy geometriai osztódásról van szó (más néven exponenciális növekedés), amelyben a osztódás exponenciális mértékben történik (2, 4, 8 és így tovább). A számtan nyelvén ez így írható le: 2 = 2^1
4 = 2^2 8 = 2^3
A hatványkitevőket megvizsgálva észrevehetjük, hogy megegyeznek az alakzatok dimenzióival: 1, 2 és 3.
Csináljuk meg ugyanezt egy fraktállal, a Sierpinski háromszöggel. Ha megfelezzük a magassága, majd az alapja felénél, csak három másolatot kapunk (mivel a középső rész nem tartozik a Sierpinksi háromszögbe). Ezután már csak egy z hatványkitevő kellene, amivel 2^z = 3. 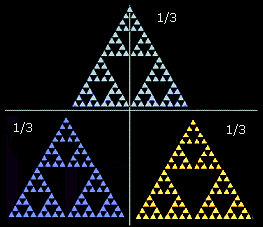
13. ábra: a Sierpinski háromszög felosztása
A Sierpinski háromszög nem egydimenziós, mivel a 3 > 2 (2^1), de nem is kétdimenziós, mert a 3 < 4 (2^2). Ezért a dimenziója valahol 1 és 2 között kell, hogy legyen. Nos, egész közel van ehhez: 1.58496250072115618145373894395 :)
Egy másfajta geometria
A fraktál, avagy tört dimenzió olyasvalami, ami nem létezik, és nem is értelmezhető az elemi geometria világában. Egy olyan területet tár elénk, ahol az euklédeszi tételek legalább egyike nem érvényesül (ezeket a tételeket a görög matematikus a Krisztus előtti 4. században írta le), s ahol más matematikai valóságok lépnek előtérbe. Így megkülönböztethetünk két fő geometria-típust: Az euklédeszi és a nem euklédeszi geometriát :) Az első kategóriához tartozik a síkmértan, a térmértan, a trigonometria, az ábrázoló geometria, a projektív geometria, az analitikus geometria és a differenciál geometria. A másodikhoz kategóriához pedig a hiperbolikus geometria, az elliptikus geometria és a fraktál geometria.
***
Miért hívják a fraktálokat "fraktáloknak"?
A "fraktál" szó a latin "fractus"-ból ered, ami töredezettet, vagy egyszerűbben töröttet jelent, ami találó szó egy tört dimenziójú tárgyra. Benoît Mandelbrot társította a fraktálokkal ezt az elnevezést még 1975-ben. A fraktálok tanulmányozását rendszerint fraktál geometriának is nevezik.

14. ábra: Egy fraktál a Mandelbrot szélénél *** Mitől olyan színesek a fraktálok? :)
A fraktálok úgy kapják a "mintázatukat" és színeiket, hogy adott színskálát rendelünk a pontjaikhoz a tulajdonságaiktól függően. Tulajdonképpen ez az egyetlen mód, hogy megnézzük őket. Több lehetőségünk is van a színkódok hozzárendeléséhez:
Az első eset az alakzaton belül történhet, a második az alakzaton kívül, a harmadik és negyedik a széleknél.
Ha nem lennének ezek a mesterséges szín hozzárendelések, akkor a fraktálok úgy néznének ki, mint bármely más egyszerű, nem igazán attraktív kép.

15. ábra: Egyszerű Mandelbrot halmaz
A cikk következő részében mélyebben belemegyek majd a fraktálok matematikájába, a komplex számokon át a káosz elméletig... szóval folyt. köv :)
Forrás: Juan Luis Martínez - The Nature Of Fractals
|
Navigáció |
Írások száma:
58 |
Kategóriák: |
 Ezoterika (
9 )
Ezoterika (
9 ) |
 Fantasy (
6 )
Fantasy (
6 ) |
 Filmek (
2 )
Filmek (
2 ) |
 Filozófia (
11 )
Filozófia (
11 ) |
 Gasztronómia (
1 )
Gasztronómia (
1 ) |
 Gyógyítás (
5 )
Gyógyítás (
5 ) |
 Könyvek (
4 )
Könyvek (
4 ) |
 Mitológia (
7 )
Mitológia (
7 ) |
 Művészet (
6 )
Művészet (
6 ) |
 Novella (
19 )
Novella (
19 ) |
 Sci-fi (
3 )
Sci-fi (
3 ) |
 Sorozatok (
2 )
Sorozatok (
2 ) |
 Természet (
11 )
Természet (
11 ) |
 Történelem (
8 )
Történelem (
8 ) |
 Tudomány (
9 )
Tudomány (
9 ) |
 Versek (
14 )
Versek (
14 ) |
Partnereink |