
| << Vissza |
| A fraktálok természete 2. |
| Teimel - 2007-08-30 14:25:00 |
| Tudomány |
|
Nem csak matematika...
A fraktálok matematikai entitások, bár túlnőnek ezen a fogalomkörön. Az első példák a jelenségre matematikai ábrák voltak, mint a Cantor köd, a Koch görbe (1904) és a Sierpinski háromszög. Ezt követte Gaston Julia és Pierre Fatou munkássága a Julia halmazú fraktálokon (1918-19), majd pár évtizeddel később Benoît Mandelbrot és más elmés tudós-matematikus tanulmánya a Mandelbrot halmazról, valamint ún. különös attraktorokról és bifurkációkról (kettéágazódás). Persze fraktálok mindenhol vannak. Sok olyan "szokványos" létforma van, amely a felépítése, vagy a viselkedése miatt a természet fraktáljának nevezhető, még ha elsőre nem is tűnik annak. A felhők, hegységek, tengerpartok, fák és folyók a természet fraktáljai. Annyiban különböznek a matematikai megfelelőiktől, hogy végesek. Egyéb példák a fraktálokra az értéktőzsde és a népszaporulat mutatói.

16. ábra: bifurkáció (kettéágazódás) A fraktálok ezen felül átlépték a határt a művészet és a tudomány között. Manapság rengeteg művész készít nagyszerűen és tehetséggel kidolgozott képeket a matematikai megfelelőkről. A fraktálok numerikus paraméterei zenei hangokká is konvertálhatóak, amelyek így érdekes, élénk dallamokká válnak. Ezt nevezik fraktál zenének. Kattints ide egy fraktál zene bemutatóért.
Nem is olyan régen a szakértők rájöttek, hogy a fraktálok már jóval azelőtt összefonódtak a művészettel, mint ahogy a matematikai természetüket felfedezték. Évszázadokon át használtak vázák, építmények, iniciálék, és sok más ábrázoló művészeti alkotás díszítő elemeként olyan geometrialiag önismétlő mintákat, amelyek valahogy kapcsolódnak a fraktál struktúrához.
  
17., 18., 19. ábra Kelta-angolszász könyv iniciálé: Kell könyvének részlete (bal); Természeti fraktál: egy nautilusz kagylója (közép); Az Ely katedrális gótikus kupolája, Anglia (jobb). Más kutatások kimutatták, hogy sok zenei stílus az ún. 1/f hányadost követi (az 1/f zajt magyarul általában rózsazajnak nevezik), amelyet a természetbeli fraktál frekvenciákkal azonosítanak, mivel ilyeneket találtak a zajok interferenciájában és pl a folyók folyásának hangjaiban (Voss és Clark, 1975). ***
A legkomplexebb matematikai elem Habár a Mandelbrot halmazt Benoît Mandelbrot fedezte fel, Adrien Douady és J. Hubbard nevezték el róla 1982-ben. A nagyon különös alakzatot számtalan alkalommal reprodukálták már az 1980-ban számítógéppel készült első vizuális ábrázolás óta. 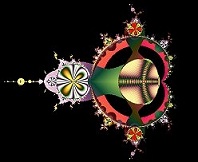
19. ábra: színes Mandelbrot halmaz A Mandelbrot halmazt leíró matematikai funkció úgy írható le, mint az összes c halmaza (ahol c egy komplex szám), úgy, hogy ismételve a z = z^2 + c (kezdve z = 0-val) nem tart a végtelenbe. Az egyenlet önmagában nagyon egyszerű, az eredményábra viszont annál komplexebb. A megjelenítéshez érdemes számítógépet használni, kézzel kicsit sokáig tartana :) ***
Gaston és Benoît : Benoît és Gaston A Mandelbrot és a Julia halmazok szorosan összefüggenek. A Mandelbrot halmaz a z = z^2 + c -t iterálja z = 0 kezdőértékkel és a c variációival. A Julia halmaz ugyanazt a függvényt iterálja, de fix c és változó z értékekkel. A Mandelbrot halmaz minden c pontja meghatározza a megfelelő Julia halmaz geometriai szerkezetét. Ha c része a Mandelbrot halmaznak, akkor a Julia halmaz kapcsolódni fog hozzá. Ha nem, akkor a Julia halmaz nem kapcsolódó pontokból fog állni.   
20 ábra: Mandelbrot-Julia átalakítás. ***
Komplex számok A Mandelbrot és Julia halmazok léte a komplex számokon alapszik. De ha már itt tartunk, nézzük meg először az imaginárius (képzetes) számokat. Két olasz matematikus, Girolamo Cardano és Raffaele Bombelli terjesztették elő mindkét számtípust a 16. században. Amint tudjuk, a negatív számoknak nincs valós számokkal kifejezhető négyzetgyöke. Mégis, a matematikusok egy képzetes értéket adtak a -1 négyzetgyökének, amelyet i -ként definiáltak. A komplex számok egy valós és egy képzetes részből állnak. A valós rész egy valós szám, pl -2, 1, 1/2, 0.2154, míg a képzetes rész egy valós szám, plusz a speciális szám, az "i", pl így: 3i. Ezek alapján egy komplex szám pl így néz ki: 2 + 3i Nem mindegyik fraktál képződik komplex számokkal dolgozó matematikai kifejezések iterációjával. Néhány az elemi geometria ábráinak iterációjával jön létre. A Sierpinski szőnyegnek pl. négyzet az alapja.   
21. ábra: balról: második, harmadik és negyedik iterációja a Sierpinski szőnyegnek *** Egyenletek, függvények, vagy képletek?
Az egyenlet olyan állítás, amely azt mutatja, hogy két matematikai kifejezés egyenlő, mint pl. x + 1 = 3 - x^2. A függvény két vagy több változó asszociációja, ahol a minden független változó minden értékéhez a függvény értelmezési tartományán belül vett függő változóknak pontosan egy értéke tartozik. Egyszerűbben, egy függvényben mint pl. f(y) = x + 1, y értéke x értékétől függ, ill. azzal együtt változik. Ebben a kifejezésben y a függő változó, x a független változó. A képlet ezzel szemben (és a mi esetünkben) egy matematikai tényt fejez ki. Például, a háromszög területének képlete: a = bh/2, ahol b az alap (base), h a magasság (height), és az a a háromszög területe (area). Visszatérve a Mandelbrot halmaz képletéhez (f(z) = z^2 + c), helyénvaló lenne függvényről beszélni. Az is igaz, hogy egyenlet, mivel a két oldal egyenlőségét mutatja a képlet, de függvény is, mert az értékek a számok egy halmazára vannak korlátozva. ***
A fraktálok és a káosz
A fraktálokat több okból kifolyólag is kapcsolatba szokták hozni a káosszal. Mindamellett, sok olyan fraktál van, aminek köze sincs a káoszhoz. Ahogy láttuk, a legtöbb korai, egyszerűbb matematikai fraktál még a 19. század végéből származik, jóval azelőttről, hogy a hatvanas években nyilvánosságra került a káoszelmélet. A számítástechnika fejlődésének köszönhetően ez az elmélet vált pár újabb típusú fraktál szülőjévé. A káosz elmélet egyik úttörője Dr. Edward Lorentz a Massachusetts-i Institute of Technology (MIT)-ból, habár Jules Henri Pointcaré már az 1830-as években előhozakodott a "pillangó effekt" elméletével. 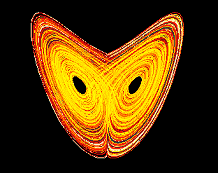
22. ábra: Lorentz attraktor Pontosan fogalmazva, a káosz elmélet az olyan nemlináris rendszerek tanulmányozásával foglalkozik, ahol a változás gyakorisága nem állandó. A kiszámíthatatlanság jellemzi őket. Az időjárás, valamint a népesség növekedése jó példák a nemlineáris rendszerekre, mindkettő fraktál. A nemlineáris rendszerekben, a rendszer minden állapota az előző állapottól függ (iteráció), és egy kis változtatás a kezdő bemeneti értékeken drámai hatással lehet a rendszer végső kimenetelében. ***
A fraktál elmélet a gyakorlatban A káosz elmélet és a fraktál geometria felfedezésének köszönhetően a tudósok (végre) megértették, hogy jópár rendszer, amit eddig teljesen kaotikusnak gondoltak, kiszámítható mintákkal rendelkeznek. A fraktál geometria egyik legjelentősebb tulajdonsága, hogy képes lemodellezni természeti jelenségeket, mint pl növényeket, felhőket, geológiai formákat, és légköri jelenségeket. A fraktál elmélet olyan helyeken is szerepet játszik, mint pl nyelvészet, pszichológia, képtömörítési eljárások, szupravezetés, áramkör kapcsolódási sémák, és más elektronikával kapcsolatos feladatok. Forrás: Juan Luis Martínez - The Nature Of Fractals
|
Navigáció |
Írások száma:
58 |
Kategóriák: |
 Ezoterika (
9 )
Ezoterika (
9 ) |
 Fantasy (
6 )
Fantasy (
6 ) |
 Filmek (
2 )
Filmek (
2 ) |
 Filozófia (
11 )
Filozófia (
11 ) |
 Gasztronómia (
1 )
Gasztronómia (
1 ) |
 Gyógyítás (
5 )
Gyógyítás (
5 ) |
 Könyvek (
4 )
Könyvek (
4 ) |
 Mitológia (
7 )
Mitológia (
7 ) |
 Művészet (
6 )
Művészet (
6 ) |
 Novella (
19 )
Novella (
19 ) |
 Sci-fi (
3 )
Sci-fi (
3 ) |
 Sorozatok (
2 )
Sorozatok (
2 ) |
 Természet (
11 )
Természet (
11 ) |
 Történelem (
8 )
Történelem (
8 ) |
 Tudomány (
9 )
Tudomány (
9 ) |
 Versek (
14 )
Versek (
14 ) |
Partnereink |

